As regular visitors to the blog know, we're always investigating potential ways to improve service through research and data analysis. While we know (and have examined on the blog) that the payment process on-board buses and light rail vehicles slows the boarding process and influences reliability, we're still working to fully understand the precise impacts of various fare media.
Our partnership with MIT is vital to these goals. For the recent Transportation Research Board conference, MIT's Jay Gordon submitted a paper and presented his work using the MBTA's databases to examine the variance of dwell times on-board buses based on the various forms of fare media. This post will summarize his methodology and discuss a portion of his findings.
Methods
The Automated Fare Collection (AFC) database anonymously records a wide variety of information about each passenger's interaction with an MBTA device (such as fareboxes, faregates, fare vending machines, etc.). Additionally, the MBTA's Automated Vehicle Location (AVL) database records the location of each MBTA vehicle via the on-board GPS both each minute and whenever the vehicle reaches a timepoint (one of a number of stops along its route used for scheduling purposes). The database also records the announcements made for each stop, and the route and destination recorded by the on-board bus software. These two sources are correlated together by the ODX model to infer the precise location and time of each boarding (96% of boardings throughout the MBTA system are successfully inferred).
The duration of each transaction is not measured by the MBTA's equipment. To estimate it, Jay used the time between consecutive transactions (the difference between transaction time 1 and transaction time 2) at a stop to estimate each transaction's duration. Jay explains in his paper:
If O is the observed duration between the completion of a fare transaction and the completion of the previous transaction, then the unobserved fare-transaction time, F, is the difference between O and the unobserved inter-arrival time since the previous transaction's completion, or I:F = O — I
In this case F is the amount of time that the customer spent interacting with the farebox while I is the amount of time elapsed between the completion of the previous customer's transaction and the beginning of the current customer's transaction: the interval in which the farebox was not being used.
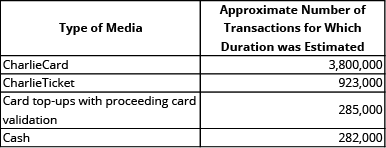
The first transaction at each stop was removed, since by definition there is a period of time when no one is attempting to pay at the farebox (when the bus is traveling between stops and opening doors). The resulting dataset could still include time periods when the bus was stopped but no one was in the process of paying; for example, if a bus is waiting at a traffic signal or a terminal station and people are walking up one-by-one rather than queueing, but these examples should have a minimal impact on the results because they should affect all fare media equally. This process produced the following totals by type of fare media:
Results
This figure shows the distribution of the durations of each observation. This includes box plots with the first, second, and third quartiles of each distribution, and “whiskers” indicating 1.5 times each distribution's inter-quartile range (IQR).
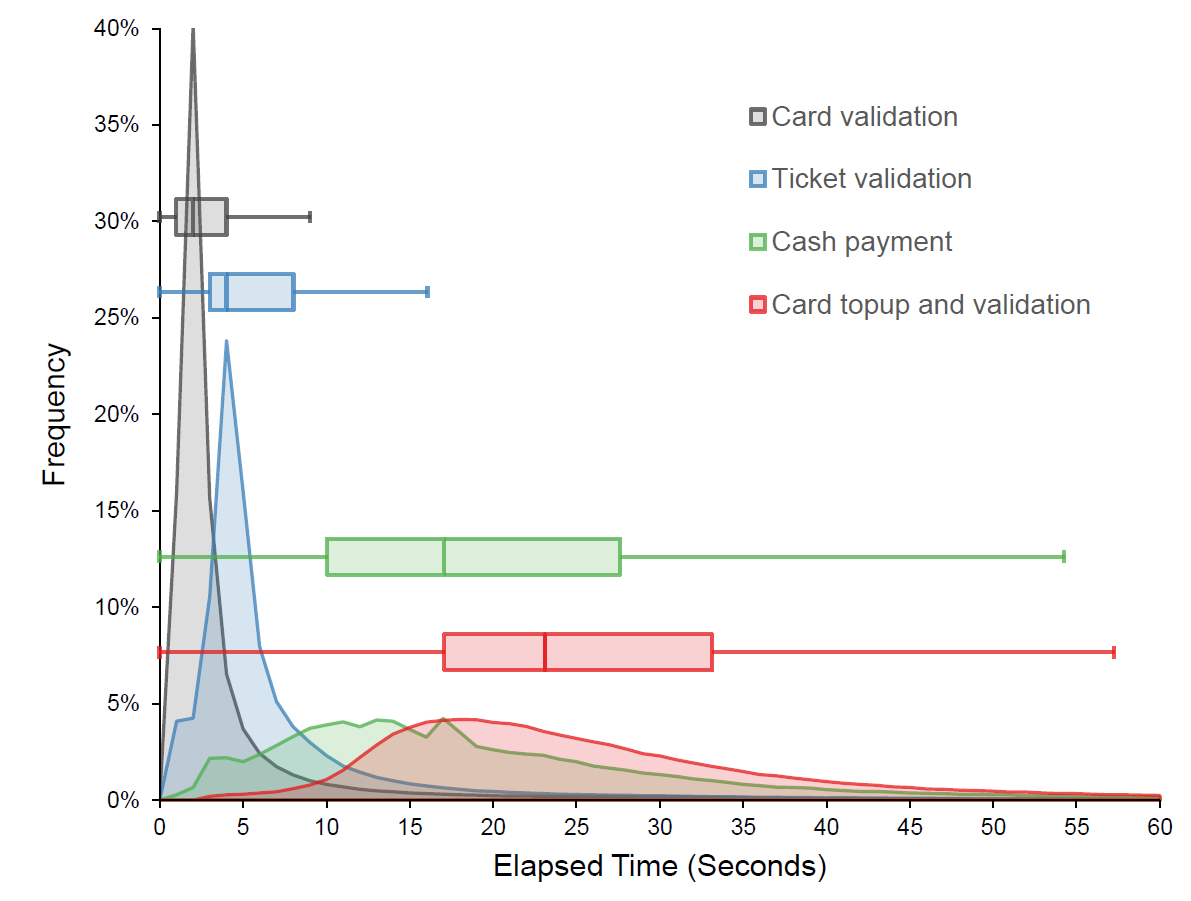
This chart and research is interesting not only because it reveals the average transaction times for each media, but also because it shows the distribution and level of variance of each. Any bus rider will tell you that card and ticket transactions are of much shorter duration than cash and top-up transactions, but they also exhibit a much smaller variance — meaning that just a few of these transactions could have either a fairly small or a fairly big impact on dwell times. For routes and times where cash and top-up payments are more common, this variance can negatively affect reliability and headways. To put this another way, if card top-ups had the same median duration but a much smaller variance, they would increase dwell times the same amount as they currently do on average but would be less likely to induce bus bunching, plus these times could be more easily accounted for in the schedule so that buses were more reliable.
Jay's research took this data further and applied the estimated impacts of various media both spatially over the bus network and temporally throughout the day. Stay tuned for a future blog post examining these additional steps.

